16.6 補数

この項ではコンピュータの基礎である補数の考え方とその利用例について説明します。

16.6.1 補数とは何か

ある定数値 $x$ に対して $y$ を足します。この時

$x + y$ の結果、 $x$ の桁をあげる事となる $y$
$x + y$ の結果、 $x$ の現在の桁で最大の数値となる $y$

をどちらも共に、補数と言い、1 を特に真補数、2 を特に擬補数と言います。補数には、この通り二つの種類があります。そしてまた、補数は、基底の数(何進数か)によって変動します。例えば 10 進数においては、10 という単位で桁が上がるので、1. のことを 10 の補数と言い、10 進数において 2. のことを 9 の補数と言います。続けて 2 進数においては、2 という単位で桁が上がるので、1. のことを 2 の補数と言い、2進数において 2. のことを 1 の補数と言います。つまり、ある値の $a$ の補数と言われた場合、そのある値は $a$ または $a + 1$ を基数とする値であり、 $a$ または $a + 1$ 進数のある値に対して桁上がりとなる値(真補数)、その桁の最大値となる値(擬補数)を補数と言います。

16.6.2 補数を求める

10 進数

10 進数の補数の求め方は直感的であるため、比較的容易です。例えば、 $5$ という 10 進数値があるとします。これに対する 9 の補数は $5 + x = 9$ より $4$ です。またこれに対する 10 の補数は $5 + x = 10$ より $5$ です。次に、 $15$ という 10 進数値があるとします。これに対する 9 の補数は $15 + x = 99$ より $84$ です。またこれに対する 10 の補数は $15 + x = 100$ より $85$ です。

2 進数

2 進数における補数表現の考え方はコンピューターでとてもよく利用される手法です。例えば $ 011_{(2)} $ という 2 進数値があるとします($_{(2)} $ は 2 進数値であることを表します)。これに対する 1 の補数は $100$ です。またこれに対する 2 の補数は $ 101_{(2)} $ です。なぜこの様になるのかは順を追えば理解できるはずです。

当然ながら二進数の世界では、1 つの桁が表せる種類が 2 通りしかありません。$ 0_{(2)} $ もしくは $ 1_{(2)} $ のみです。この次の値を表すには桁を上げるしかありません。 $ 011_{(2)} $ を二進数における 3 桁であると捉えると、この 3 桁で表せる最大の数値は $ 111_{(2)} $ですから、つまり、1 の補数は以下の様にして考える事ができます。 \[ 011_{(2)} + x = 111_{(2)} \] この時の $x$ が 1 の補数です。$ 011_{(2)} $ に何を足せば $ 111_{(2)} $ になるのでしょうか。$ 100_{(2)} $ですね。よって、1 の補数は $ 100_{(2)} $ です。

次に 2 の補数について考えます。といっても、ここまで理解できていれば全く難しいことはありません。 2 の補数というのは、二進数において桁を上げる数値なので、単純に 1 の補数 + 1 の値になるはずです。 1 の補数は $ 100_{(2)} $ でしたから、それに 1 を加えた $ 101_{(2)} $ を $ 011_{(2)} $ に加える事で桁上がりが起きます。よって、2 の補数は $ 101_{(2)} $ です。

これがわかると、慣例として言われる、「ある値のビット反転 + 1 がある値の 2 の補数である」という法則にも納得が行くはずです。まずビット反転とは、単純に全てのビットが反転するという事です。つまり $ 1_{(2)} $ だったら $ 0_{(2)} $ になるし、$ 0_{(2)} $ だったら$ 1_{(2)} $ になるという事です。例えば、$ 1010_{(2)} $ という値をビット反転したら $ 0101_{(2)} $、$ 1100_{(2)} $ という値をビット反転したら$ 0011_{(2)} $です。

「ある値のビット反転 + 1 がある値の 2 の補数である」という話に戻します。先ほどの例の数値$ 011_{(2)} $ を再度用います。この値をビット反転した値は、$ 100_{(2)} $です。これは、先ほど求めた 1 の補数です。これに 1 を加えると先ほど求めた 2 の補数ですね($ 101_{(2)} $)。これが、「ある値のビット反転 + 1 がある値 2 の補数である」の仕組みです。

16.6.3 何に使える/使われているのか

結論から言えば、広義の意味でのコンピュータによる減算で, 補数は利用されています。コンピューターによる減算は回路を簡素化するために、加算で行われています。例えば $x - x = y$ で、 $y$ を加算のみで演算しようとすると以下の様になります。 \[ x + (x の 2 の補数) から桁上がりの部分を捨てた値 = y \] 実際に値を入れると分かりやすいでしょう。 $x$ を $ 011_{(2)} $とすると、 \[ 011_{(2)} + (011_{(2)} の 2 の補数) から桁上がりの部分を捨てた値 = y \] となります。次に、 $011\_{(2)}$ の 2 の補数を求めると以下の様になります。 \[ 011_{(2)} + 101_{(2)} から桁上がりの部分を捨てた値 = y \] これを演算します。 $+$ 表記があるので、加算を行います。 \[ 1000_{(2)} から桁上がりの部分を捨てた値 = y \] 後は、「桁上がりの部分を捨てた値」について処理すれば完了です。 $011\_{(2)} + 101\_{(2)}$ の加算処理によって、ここまで 3 桁であったものが 4 桁の 2 進数値になりました。「桁上がりの部分」とは、この時$ 1000_{(2)} $の先頭の$ 1_{(2)} $ を示します。 \[ 000_{(2)} = y \] このようにして、演算結果である $0$ を $-$ を使わずに加算だけで求める事ができました。別の値でもやってみましょう。

例えば、 $5 - 3$ を上記の手法で解いてみます。 $5$ は二進数表記で$ 101_{(2)} $、 $3$ は二進数表記で$ 011_{(2)} $ です。 \[ 101_{(2)} + (011_{(2)} の 2 の補数) から桁上がりの部分を捨てた値 = y \] $ (011_{(2)} の 2 の補数) $ を展開すると以下の様になります。 \[ 101_{(2)} + 101_{(2)} から桁上がりの部分を捨てた値 = y \] $ 101_{(2)} + 101_{(2)} $ の加算を行います。 \[ 1010_{(2)} から桁上がりの部分を捨てた値 = y \] 桁上がりを捨てます。 \[ 0010_{(2)} \] $ 0010_{(2)} $ は 10 進数で $2$ です。正しく計算が行えました。
このようなコンピューターの基本的な演算に利用される補数という概念ですが、この性質を利用したビット演算などが有名です。例えば、次の一行は、右端に立っているビットのみを残してそのほかを全て $ 0_{(2)} $ にするコードです。

x & (-x)

コード中の-によって、xの内部では補数表現によって値が表現されます。例えば、x が 3 ビットのデータで、中には $ 011_{(2)} $ が入っているとしてこの演算を見てみると一目瞭然です。

0b011 & 0b101

これで0b001が残ることがわかります。別の値でもやってみましょう。xを 6 ビットとして中身を $101010$ としてみます。

0b101010 & 0b010110

これも0b000010というように最後のビットを取ることができました。これまでの説明からもわかるように、元の値のビット反転 + $1$ が元の値のマイナスを示すという性質を利用していますね。

16.6.4 自分で四則演算子を作ってみよう

補数に関する話をしましたので、これを利用して C++ 言語に用意されている+, -, *, /等を使わずに、ビット演算のみで同様の計算処理を行う関数を簡単に作ってみましょう¹。以下、下付き文字 $_{(2)}$ が付与されている数字は 2 進値、そうでない数字は 10 進値として話を進めます。

加算

まずは加算から作っていきます。1 ビットの足し算をどのように論理演算で実現できるか考えます。 1 ビット同士の加算では、最大 $1_{(2)} + 1_{(2)}$ のときに繰り上がって$10_{(2)}$ となりますから、結果の取得には最低でも 2 ビット、まずは必要であることがわかります。さらに $2^{0}$ の桁の値を $Y^{0}$ 、$2^{1}$ の桁の値を $Y^{1}$ としたとき、次の表の通りにその演算結果が得られることで、加算が再現できたといえます。

左辺	右辺	$Y^1$	$Y^0$
$0_{(2)}$	$0_{(2)}$	$0_{(2)}$	$0_{(2)}$
$0_{(2)}$	$1_{(2)}$	$0_{(2)}$	$1_{(2)}$
$1_{(2)}$	$0_{(2)}$	$0_{(2)}$	$1_{(2)}$
$1_{(2)}$	$1_{(2)}$	$1_{(2)}$	$0_{(2)}$

ここで $Y^0$ の結果について着目すると、左辺と右辺の排他的論理和を取ればその通りになることが考えられます。よって、1 ビット目の結果を得るには、左辺と右辺の排他的論理和を取れば良いことがわかりました。次に $Y^1$ の結果について着目すると、左辺と右辺の論理積を取ればその通りになることが考えられます。よって、2 ビット目の結果を得るには、左辺と右辺の論理積を取れば良いことがわかりました。この原理をコードに落とし込むと、次のように実装できます。

#include <type_traits>

namespace TPLCXX17 {

#if 1
template <class Integral, std::enable_if_t<std::is_integral<Integral>::value, std::nullptr_t> = nullptr>
constexpr Integral add(Integral lhs, Integral rhs) noexcept
{
    for (Integral carry = (lhs & rhs) << 1; rhs; carry = (lhs & rhs) << 1) {
        lhs ^= rhs;
        rhs = carry;
    }
    return lhs;
}
#else // 再起バージョン
template <class Integral, std::enable_if_t<std::is_integral<Integral>::value, std::nullptr_t> = nullptr>
constexpr Integral add(const Integral lhs, const Integral rhs) noexcept
{
    return rhs ? add(lhs ^ rhs, (lhs & rhs) << 1) : lhs;
}
#endif

} // namespace TPLCXX17

まずrhsが $0$ である場合、何もする必要はないですね。 carryには前述した通り、左辺と右辺の論理積によって次の桁の値、つまり繰り上がりの値を予め入れておきます。繰り上がりは次の桁で作用させなければならないので、1 ビットシフトして格納します。ループ内では前述した通り、左辺と右辺の排他的論理和によって、いまループ内で着目している桁の値を得てlhsにそのまま格納します。その後、事前に取得しておいた繰り上がりの値をrhsに格納し、次のループで同じように繰り返します。このとき以前の加算時に繰り上がりが起きていなければ(すなわちrhsが $0$ であれば)、ループは終了し、加算処理は完了となります。これが単に、小学校で習う足し算の筆算と全く同じことをしていることに気づくととても呆気ないですが、実際の CPU でもこれが電気回路化されて加算を実現しているのですから、筆算も中々侮れません。

減算

減算は、前述した通り補数表現とその値を用いた加算によって実現します。もうすでに私たちは加算器を手に入れていますから、減算器のためにすることは殆どありません。右辺を単にその値の真補数に変換してあげれば良いだけです。

#include <type_traits>
#include <utility>

namespace TPLCXX17 {

template <class Integral, std::enable_if_t<std::is_integral<Integral>::value, std::nullptr_t> = nullptr>
constexpr Integral sub(Integral lhs, Integral rhs) noexcept
{
    return add(std::move(lhs), add(~rhs, Integral(1)));
}

} // namespace TPLCXX17

積算

積算は一番シンプルな方法として、筆算のように加算を繰り返すことで実現できます。

#include <cstdint>
#include <type_traits>
#include <utility>

namespace TPLCXX17 {
namespace detail {

#if 1
template <class Integral, std::enable_if_t<std::is_integral<Integral>::value, std::nullptr_t> = nullptr>
constexpr Integral mul_impl(Integral lhs, Integral rhs) noexcept
{
    Integral carry = 0;
    while (rhs) {
        if (rhs & 1) carry = add(carry, lhs);
        rhs >>= 1;
        lhs <<= 1;
    }
    return carry;
}
#else // 再起バージョン
template <class Integral, std::enable_if_t<std::is_integral<Integral>::value, std::nullptr_t> = nullptr>
constexpr Integral mul_impl(Integral lhs, Integral rhs, Integral carry = 0) noexcept
{
    return rhs ? ((rhs & 1) ? mul_impl(lhs << 1, rhs >> 1, add(carry, lhs)) : mul_impl(lhs << 1, rhs >> 1, carry)) : carry;
}
#endif

template <std::size_t>
struct msb_mask;
template <>
struct msb_mask<1> : std::integral_constant<std::uint8_t, 0x80> {};
template <>
struct msb_mask<2> : std::integral_constant<std::uint16_t, 0x8000> {};
template <>
struct msb_mask<4> : std::integral_constant<std::uint32_t, 0x80000000> {};
template <>
struct msb_mask<8> : std::integral_constant<std::uint64_t, 0x8000000000000000> {};

template <class TraitsType, class T, class Fn>
constexpr T transigned_invoke(T&& lhs, T&& rhs, Fn&& fn) noexcept
{
    typedef typename TraitsType::type type;
    constexpr type one = type(1);

    if (lhs & rhs & TraitsType::value) return std::invoke(std::forward<Fn>(fn), add(~lhs, one), add(~rhs, one));
    else if (lhs & TraitsType::value) return add(~std::invoke(std::forward<Fn>(fn), add(~lhs, one), rhs), one);
    else return std::invoke(std::forward<Fn>(fn), std::forward<T>(lhs), std::forward<T>(rhs));
}

} // namespace detail

template <class Integral, std::enable_if_t<std::conjunction_v<std::is_integral<Integral>, std::is_unsigned<Integral>>, std::nullptr_t> = nullptr>
constexpr Integral mul(Integral lhs, Integral rhs) noexcept
{
    return lhs && rhs ? detail::mul_impl(std::move(lhs), std::move(rhs)) : 0;
}

template <class Integral, std::enable_if_t<std::conjunction_v<std::is_integral<Integral>, std::is_signed<Integral>>, std::nullptr_t> = nullptr>
constexpr Integral mul(Integral lhs, Integral rhs) noexcept
{
    if (!(lhs && rhs)) return 0;

    typedef detail::msb_mask<sizeof(Integral)> traits_type;

    return 
        detail::template transigned_invoke<traits_type>(std::move(lhs), std::move(rhs), [](auto&& inlhs, auto&& inrhs) { 
            return detail::mul_impl(std::forward<decltype(inlhs)>(inlhs), std::forward<decltype(inrhs)>(inrhs)); 
        });
}

} // namespace TPLCXX17

mul_implが主な積算の実装で、1 桁ずつ加算していることがわかります。mulでは引数が負数であった場合と、引数のどちらか一方、または両方が $0$ である場合の処理を行なっています。特にmul_implに対して負数を渡すと、算術シフトがアーキテクチャ上で実装されている場合に無限ループとなってしまいますから、std::is_signed_v<Integral> == trueであるとき、mulの中で引数のうちに負数を含む場合、その値を正数にして一度計算し、その後に符号を付与して返すようにしています。負数かどうかのチェックは比較演算子を利用しても良いですが、今回はビット演算のみを利用することとしていますので、MSB と論理積をとって判定します。その際対象となる型のサイズによってビットマスクを変えなければなりませんので、簡易的ですがmsb_maskとしてその差分を吸収しています。

除算

除算は有名なものでは非回復型除算(引き放し法)というものがあります。非回復型除算は、回復型除算(引き戻し法)から"回復"をその計算過程の性質から見抜いて排除した除算の方法です。まず回復型除算について説明します。私たちは例えば $1729 \div 13$ を筆算で計算しようとしたときに、被除数の $7$ の位置に $1$ を立てて $17-13$ を計算し、部分剰余 $4$ を得てから $2$ を降ろして $42$ という値を得ます。この次に被除数の $2$ の位置に立てるべき数は $3$ ですが、多く見積もりすぎて $4$ を立ててしまったとしましょう。すると $13 \times 4 = 52$ となり $42 - 52 = -10$ という部分剰余を得ることになります。従って、このときの除数を元に戻して $3$ に修正してやり直すことになります。いまは値を 10 進値として計算していましたから、仮定する商の値は $0$ から $9$ の値を取りうることになります。これを 2 進法で計算すると考えると、仮定する商の値は $0$ か $1$ となりますからまず $1$ を仮定して減算を行い、部分剰余が負数であれば商を $0$ に、そうでなければ $1$ にすれば良いということが考えられます。そして次のサイクルで部分剰余が負数であった場合、部分剰余に除数を加えて元に戻すことで計算を続行します。これが回復型除算です。この動作による除算は、除数、被除数ともに $N$ ビットとした場合、減算の結果が一度も負数とならなければ $N$ サイクルで計算が終了しますが、反対に常に減算の結果が負数となり、次のサイクルで元に戻すという操作が必要になると $2N$ サイクルを必要とすることになります。

次に非回復型除算について説明します。$N=4$, 被除数を $7=0111_{(2)}$, 除数を $3=0011_{(2)}$ とします。被除数の MSB と除数の LSB のビット位置を合わせるために、被除数を $0000111_{(2)} = 7$, 除数を 3 ビットシフト($=\times 2^3$)して $0011000_{(2)} = 24$ とします。 $7 - 24 = -17$ であり計算結果が負数ですから、商の MSB は $0_{(2)}$ となります。ここまでは、回復型除算と変わりません。回復型除算はこの後に回復を行い、$7 - 12 = 0000111_{(2)} - 0001100_{(2)} = 7 - 3 \times 2^2$ を計算することになりますが、 $3\times 2^2 = 3\times 2^3 \div 2$ なので、$7 - 3 \times 2^{3} + 3 \times 2^{2} = 7 - 3 \times 2^{2}$ がいえます。つまり剰余 $-17$ に $3\times 2^2$ を加えたものと同じであることが言えます($-17 + 3 \times 2^2 = -17 + 12 = -5$)。よってそのビットの商が $0$ であるとき、次のビットの計算は減算ではなく、加算をすれば良いことが言えます。これが非回復法です。

ここでの結果は $-5$ だったため、商の MSB から一つ右のビットも $0_{(2)}$ となります。先の説明の通り、剰余が負数である場合、次の計算で加算を行いますから $-5+3\times 2^1 = -5+6=1$ となり剰余が正数であるため、商の 3 ビット目は $1_{(2)}$ になります。先の計算結果が正数であったため、次は減算を行います。$1-3=-2$ となり、剰余が負数となるため LSB は $0_{(2)}$ となります。以上から、結果として $0010_{(2)}$ が得られました。

あとはこれをコードに落とし込んでいくだけですが、アクティビティ図があると流れが分かりやすいかと思いますので、まず以下に示します。

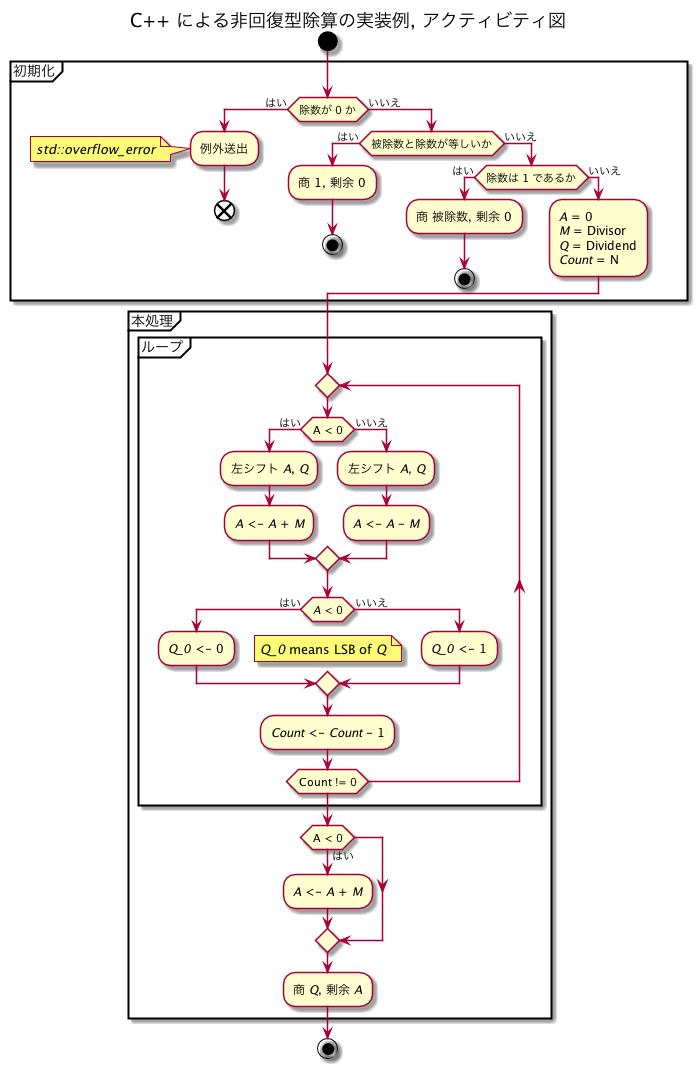
non restoring div algo

次にコードを示します。

#include <bitset>
#include <string>
#include <utility>
#include <type_traits>
#include <iostream>
#include <srook/bit/algorithm/nlz.hpp>

namespace TPLCXX17 {
namespace detail {

template <std::size_t x, std::size_t y>
struct msbit_impl {
    template <class T>
    static constexpr T apply(T i) noexcept { return msbit_impl<(x << 1), y>::apply(i | (i >> x)); }
};

template <std::size_t x>
struct msbit_impl<x, x> {
    template <class T>
    static constexpr T apply(T i) noexcept { return i |= (i >> x), i - (i >> 1); }
};

template <class T>
constexpr T msbit(T x) noexcept 
{ 
    return msbit_impl<1, (mul(sizeof(T), std::size_t(CHAR_BIT)) >> 1)>::apply(std::move(x)); // MSB から最初のビットだけ残す
} 

template <class Integral>
struct integrals_shifted {
    constexpr integrals_shifted(Integral md) 
        : maxdigit(std::move(md)), mask(init_mask(srook::bit::algorithm::nlz(maxdigit)))
    {
        std::cout << "digit bit: " << std::bitset<mul(sizeof(Integral), std::size_t(CHAR_BIT))>(maxdigit) << std::endl;
        std::cout << "mask bit: " << std::bitset<mul(sizeof(Integral), std::size_t(CHAR_BIT))>(mask) << std::endl;
    }

    constexpr std::pair<Integral, Integral> shift(const Integral x, const Integral y) const noexcept
    {
        std::cout << "a= " << std::bitset<sizeof(Integral) * CHAR_BIT>(~mask & ((x << 1) | bool(y & maxdigit))) << ", ";
        std::cout << "q= " << std::bitset<sizeof(Integral) * CHAR_BIT>(~mask & ((y & ~maxdigit) << 1)) << std::endl;
        return { ~mask & ((x << 1) | bool(y & maxdigit)), ~mask & ((y & ~maxdigit) << 1) };
    }

    const Integral maxdigit;
    Integral mask;
private:
    constexpr Integral init_mask(std::size_t nl, Integral m = 0) const noexcept // 計算に不要なビットを排除するためのマスクを生成する
    {
        return nl ? init_mask(sub(nl, std::size_t(1)), (m | maxdigit) << 1) : m;
    }
};

} // namespace detail

template <class Integral, std::enable_if_t<std::conjunction_v<std::is_integral<Integral>, std::is_unsigned<Integral>>, std::nullptr_t> = nullptr>
constexpr std::pair<Integral, Integral> div(Integral dividend, Integral divisor)
{
    if (!divisor) throw std::overflow_error(__func__ + std::string("Divide by zero")); 
    else if (dividend == divisor) return { 1, 0 };
    else if (divisor == 1) return { dividend, 0 };

    constexpr std::size_t bitsize = mul(sizeof(Integral), std::size_t(CHAR_BIT));
    typedef std::bitset<bitsize> bitset_t;

    Integral a = Integral(0), q = dividend, m = divisor;
    std::cout << "a: " << bitset_t(a) << ", q: " << bitset_t(q) << std::endl;
    detail::integrals_shifted<Integral> shifted(detail::msbit(std::max(dividend, divisor)));

    for (std::size_t i = sub(static_cast<Integral>(bitsize), srook::bit::algorithm::nlz(std::max(dividend, divisor))); i; i = sub(static_cast<Integral>(i), Integral(1))) {
        if (a & shifted.maxdigit) {
            std::tie(a, q) = shifted.shift(a, q);
            a = ~shifted.mask & add(a, m);
            std::cout << "add a + m: a = " << bitset_t(a) << std::endl; 
        } else {
            std::tie(a, q) = shifted.shift(a, q);
            a = add(a, add(Integral(~shifted.mask & Integral(~m)), Integral(1)));
            std::cout << "add a - m: a = " << bitset_t(a) << std::endl;
        }

        if (a & shifted.maxdigit) {
            std::cout << "q0 to 0: q = " << bitset_t(q & ~1) << std::endl;
            q &= ~1;
        } else {
            std::cout << "q0 to 1: q = " << bitset_t(q | 1) << std::endl;
            q |= 1;
        }
        std::cout << std::endl;
    }
    if (a & shifted.maxdigit) {
        a = ~shifted.mask & add(a, m);
    }
    return { q, a };
}

template <class Integral, std::enable_if_t<std::conjunction_v<std::is_integral<Integral>, std::is_signed<Integral>>, std::nullptr_t> = nullptr>
constexpr std::pair<Integral, Integral> div(Integral dividend, Integral divisor)
{
    typedef detail::msb_mask<sizeof(Integral)> mask_type;
    typedef std::make_unsigned_t<Integral> unsigned_type;

    constexpr Integral one = Integral(1);
    constexpr unsigned_type uone = unsigned_type(1);

    if (dividend & divisor & mask_type::value) {
        return div(unsigned_type(add(~dividend, one)), unsigned_type(add(~divisor, one)));
    } else if (dividend & mask_type::value) {
        auto [q, a] = div(unsigned_type(add(~dividend, one)), unsigned_type(divisor));
        return { add(~q, uone), a };
    } else if (divisor & mask_type::value) {
        auto [q, a] = div(unsigned_type(dividend), unsigned_type(add(~divisor, one)));
        return { add(~q, uone), a };
    } else {
        return div(unsigned_type(dividend), unsigned_type(divisor));
    }
}

} // namespace TPLCXX17

まず冒頭で<srook/bit/algorithm/nlz.hpp>というものをインクルードしていますが、これは著者が実装したnlzというビットカウントの関数を利用するために行なっています。 nlzとは MSB 側から見て何ビット $0_{(2)}$ が並んでいるか数えるものです。この実装に関する説明は本項の内容の範囲外となりますので省きますが、もし興味があれば実装を見てみてください。
テンプレート関数divは、与えられた引数が符号付きか符号なしかで呼び分けられます。符号付きの場合、与えられた値が前述したmulのように負数であるかをチェックし、負数であった場合、一度すべてそれを正数にしてから符号なしとしてdivを呼び出します。その後、左辺と右辺の正負の組み合わせから、計算結果として正しくなるよう符号を付与して返します。符号なしの場合、本除算処理のdivが呼び出されます。
まず除数が $0$ である場合は $0$ 割の例外を送出するようにしています。次に被除数と除数が同じである場合は商が $1$, 剰余が $0$ であることが自明ですから、解としてそれを返します。次に、除数が $1$ である場合、商は被除数そのものと同じで剰余が $0$ であることが自明ですから、解としてそれを返します。いずれも該当しない場合、本除算処理に入ります。まず各値をセットしてdetail::integrals_shifted<Integral>を生成しています。ここには、被除数、除数のうち最大の値の MSB から最初のビットのみ立っている値を入れます。detail::integrals_shifted<Integral>のコンストラクタでは、その値そのもの(maxdigit)と、その値より大きい桁のビットを全て $1_{(2)}$ としたmaskを構築します。ループの内容はフローの流れの通りですが、各計算間で、ループの前に構築したdetail::integrals_shifted<Integral>::maskでマスクをかけ、必要としないビットを全て $0_{(2)}$ に倒します。また、detail::integrals_shifted<Integral>::shift()を使って、2 変数間における左シフト処理を行います。フロー通りに計算を終えると、商と剰余のペアを返します。
計算過程が分かりやすいように、各計算過程を出力するようにしました。これを例えば、次のように利用します。

template <class Integral>
void print_div(Integral lhs, Integral rhs)
{
    typedef std::conditional_t<
        std::disjunction_v<std::is_same<Integral, unsigned char>, std::is_same<Integral, signed char>, std::is_same<Integral, char>>,
        int, Integral
    > cast_type;

    auto [q, r] = TPLCXX17::div(lhs, rhs);
    std::cout << static_cast<cast_type>(lhs) << " / " << static_cast<cast_type>(rhs) << " = " << static_cast<cast_type>(q) << " 余り " << static_cast<cast_type>(r) << std::endl;
}

int main()
{
    print_div(1729, 13);
    print_div(std::uint8_t(97), std::uint8_t(3));
}

実行すると、次のような出力が得られます。

a: 00000000000000000000000000000000, q: 00000000000000000000011011000001
digit bit: 00000000000000000000010000000000
mask bit: 11111111111111111111100000000000
a= 00000000000000000000000000000001, q= 00000000000000000000010110000010
add a - m: a = 00000000000000000000011111110100
q0 to 0: q = 00000000000000000000010110000010

a= 00000000000000000000011111101001, q= 00000000000000000000001100000100
add a + m: a = 00000000000000000000011111110110
q0 to 0: q = 00000000000000000000001100000100

a= 00000000000000000000011111101100, q= 00000000000000000000011000001000
add a + m: a = 00000000000000000000011111111001
q0 to 0: q = 00000000000000000000011000001000

a= 00000000000000000000011111110011, q= 00000000000000000000010000010000
add a + m: a = 00000000000000000000000000000000
q0 to 1: q = 00000000000000000000010000010001

a= 00000000000000000000000000000001, q= 00000000000000000000000000100010
add a - m: a = 00000000000000000000011111110100
q0 to 0: q = 00000000000000000000000000100010

a= 00000000000000000000011111101000, q= 00000000000000000000000001000100
add a + m: a = 00000000000000000000011111110101
q0 to 0: q = 00000000000000000000000001000100

a= 00000000000000000000011111101010, q= 00000000000000000000000010001000
add a + m: a = 00000000000000000000011111110111
q0 to 0: q = 00000000000000000000000010001000

a= 00000000000000000000011111101110, q= 00000000000000000000000100010000
add a + m: a = 00000000000000000000011111111011
q0 to 0: q = 00000000000000000000000100010000

a= 00000000000000000000011111110110, q= 00000000000000000000001000100000
add a + m: a = 00000000000000000000000000000011
q0 to 1: q = 00000000000000000000001000100001

a= 00000000000000000000000000000110, q= 00000000000000000000010001000010
add a - m: a = 00000000000000000000011111111001
q0 to 0: q = 00000000000000000000010001000010

a= 00000000000000000000011111110011, q= 00000000000000000000000010000100
add a + m: a = 00000000000000000000000000000000
q0 to 1: q = 00000000000000000000000010000101

1729 / 13 = 133 余り 0
a: 00000000, q: 01100001
digit bit: 01000000
mask bit: 10000000
a= 00000001, q= 01000010
add a - m: a = 01111110
q0 to 0: q = 01000010

a= 01111101, q= 00000100
add a + m: a = 00000000
q0 to 1: q = 00000101

a= 00000000, q= 00001010
add a - m: a = 01111101
q0 to 0: q = 00001010

a= 01111010, q= 00010100
add a + m: a = 01111101
q0 to 0: q = 00010100

a= 01111010, q= 00101000
add a + m: a = 01111101
q0 to 0: q = 00101000

a= 01111010, q= 01010000
add a + m: a = 01111101
q0 to 0: q = 01010000

a= 01111011, q= 00100000
add a + m: a = 01111110
q0 to 0: q = 00100000

97 / 3 = 32 余り 1

¹. ここでは補数を実際に利用してみることを主軸としているため、各サンプル実装においてはオーバーフロー等の演算エラーに関して特に配慮していません。 ↩

左辺	右辺	\(Y^1\)	\(Y^0\)
\(0_{(2)}\)	\(0_{(2)}\)	\(0_{(2)}\)	\(0_{(2)}\)
\(0_{(2)}\)	\(1_{(2)}\)	\(0_{(2)}\)	\(1_{(2)}\)
\(1_{(2)}\)	\(0_{(2)}\)	\(0_{(2)}\)	\(1_{(2)}\)
\(1_{(2)}\)	\(1_{(2)}\)	\(1_{(2)}\)	\(0_{(2)}\)